复包络、Hilbert变换、IQ调制这三个概念经常在通信信号处理中出现，把每个单独拎出来我好像都能大概知道，但是把它们放到一起总是令我困惑——大概因为这三者都需要把实信号表示为复信号。为了厘清这三者的概念以及其之间的关系，我调研了一些资料并整理出来。我将先把他们的概念讲清楚，然后再分析这三者之间的关系。
什么是复包络（等效基带/低通信号）
通信中很重要的一个过程就是调制解调。所谓调制，就是把信息加载到特定的波上以获取更好的通信特性。解调就是从接收到的经过信道的信号中提取发射端加载的信息。根据信息是离散的还是模拟的可以分为数字调制和模拟调制。因为所有频带通信的调制方式都是把信息加载到一个正弦波的振幅$\alpha(t)$、频率$f(t)$或者相位上$\theta(t)$，所以它们可以有一个统一的表达式：
\[\begin{equation} s(t)=\alpha(t)cos[2\pi(f_c+f(t))t+\theta(t)+\phi_0]=\alpha(t)cos(2\pi f_ct + \phi(t)+\phi_0) \end{equation}\]注意这个表达式是和调制方式无关的。我们可以通过三角关系式把上式中的载波提取出来
\[\begin{equation} \label{complex_envelope} \begin{array}{} s(t)&=&\alpha(t)cos(\phi(t)+\phi_0)cos(2\pi f_ct)-\alpha(t)sin(\phi(t)+\phi_0)sin(2\pi f_ct)\\ &=& s_I(t)cos(2\pi f_ct)-s_Q(t)sin(2\pi f_ct) \end{array} \end{equation}\]上式第一项与载波同相因此称为带通信号的同相（in-phase）分量而第二项与载波差$\pi/2$的相位因此称为正交（quadrature）分量。在实际使用中，我们定义一个复信号$u(t)=s_I(t)+js_Q(t)$，那么带通信号就可以表示为
\[\begin{equation} s(t)=\Re\{u(t)e^{j2\pi f_ct}\} \end{equation}\]而其中$u(t)$就是带通信号的复包络（或者叫等效基带信号）。
以上就是带通信号复包络的定义，而这部分除了把带通信号经过数学操作化简为了另一种形式，好像并没有其他的意义。要想真正了解这么做的优势，需要结合整个通信过程来看。
我们知道描述一个信道的方法是定义其单位冲激响应$h(t)$，对于带通信道我们也可以用同样的方式定义一个复的冲激响应$h_l(t)$使得
\[\begin{equation} h(t)=2\Re\{h_l(t)e^{j2\pi f_ct}\} \end{equation}\]当我们发送$s(t)$经过信道后其理想输出为$r(t)=s(t)*h(t)$，因为$s(t)$和$h(t)$都是实数，并且其频谱$R(f)=H(f)S(f)$也是带限的。因此$r(t)$也可以用其等效基带信号来表示
\[\begin{equation} r(t)=\Re\{v(t)e^{j2\pi f_ct}\} \label{eq:eff-base-sig} \end{equation}\]至此我们已经有了发送、信道和接收的三个等效基带信号，那么这三个低通信号能做什么呢？ 我们首先来从频域（比较简单）化简一下接收信号
\[\begin{equation} \begin{array}{rl} R(f)&=&H(f)S(f)\\ &=&0.5[H_l(f-f_c)+H_l^*(-f-f_c)][U(f-f_c)+U^*(-f-f_c)] \end{array} \end{equation}\]因为$s(t)$和$h(t)$都是带通的，因此有交叉项
\[\begin{equation} H_l(f-f_c)U^*(-f-f_c)=0 \end{equation}\]和交叉项
\[\begin{equation} H_l^*(-f-f_c)U(f-f_c)=0 \end{equation}\]因此可以进一步化简
\[\begin{equation} R(f)=0.5[H_l(f-f_c)U(f-f_c)+H_l^*(-f-f_c)U^*(-f-f_c)] \label{eq:simp_rf} \end{equation}\]同时，接收信号的频谱根据$\eqref{eq:eff-base-sig}$可以表示为
\[\begin{equation} R(f)=0.5[V(f-f_c)+V^*(-f-f_c)] \label{eq:rf} \end{equation}\]把$\eqref{eq:simp_rf}$和$\eqref{eq:rf}$中正负频率分量相等可知
\[\begin{equation} V(f)=H_l(f)U(f) \end{equation}\]因此这三个低通信号的关系就建立了起来，即
\[\begin{equation} v(t)=u(t)*h_l(t) \end{equation}\]这是一个非常优美的结论，这意味着在分析一个通信系统不再依赖于载波的频率。在通信系统的仿真中，我们也不需要真的去产生一个几GHz的波（这需要至少二倍于这个频率的采样），而只需要以更低的采样率去分析等效基带信号就可以了，这可以极大的降低存储和计算成本。
Hilbert变换与解析信号
Hilbert变换的数学形式就不再这里赘述，对于它的直观概念就是把被变换的信号的所有正频率部分乘以$j$而负频率部分乘以$-j$，也就是说它的物理意义是将所有的频率分量相位推迟$90^\circ$。通过Hilbert变换我们可以定义任意实信号的$x(t)$的解析信号
\[\begin{equation} x_a(t)=x(t)+j\hat{x}(t) \label{eq:hilbert} \end{equation}\]其中$\hat{x}(t)$就是$x(t)$的Hilbert变换。根据Hilbert变换的数学性质，我们可以知道解析信号$x_a(t)$的正频率分量是原来的二倍，直流分量与原来相等而负频率分量为0。如果把解析信号调制到高频载波上，其占用的带宽只有原信号的二分之一。由此可以引出Hilbert变换的第一个应用——单边带（SSB，Single Side-Band）调制。
Hilbert变换应用于SSB调制
为了更形象的说明问题，这里以AudioMnist数据集中一个发出“seven”的语音信号为实例。下图展示了这个信号的部分时域波形以及它的Fourier变换。
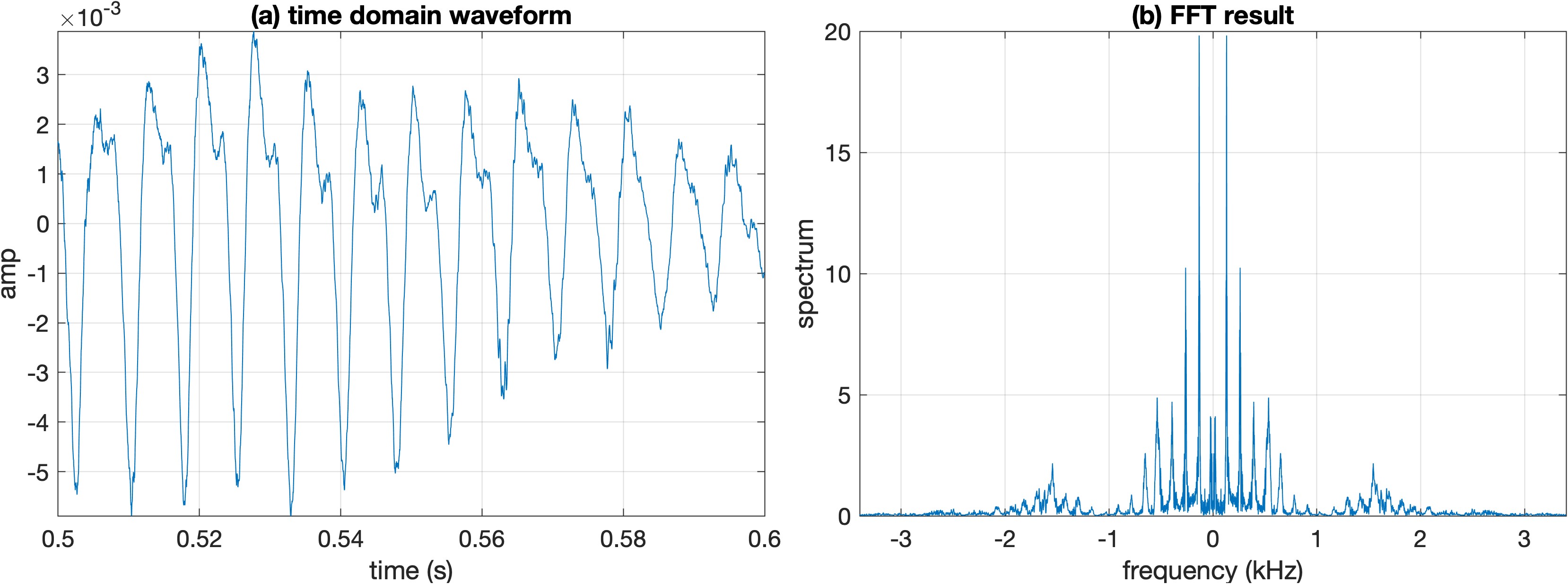（a）示例信号的0.5s至0.6s的时域波形；（b）整段信号的FFT结果（频率限制在$\pm$3.4 kHz，对应于人声的主要频段）。
根据公式$\eqref{eq:hilbert}$得到这段信号的解析信号，结果如下图所示
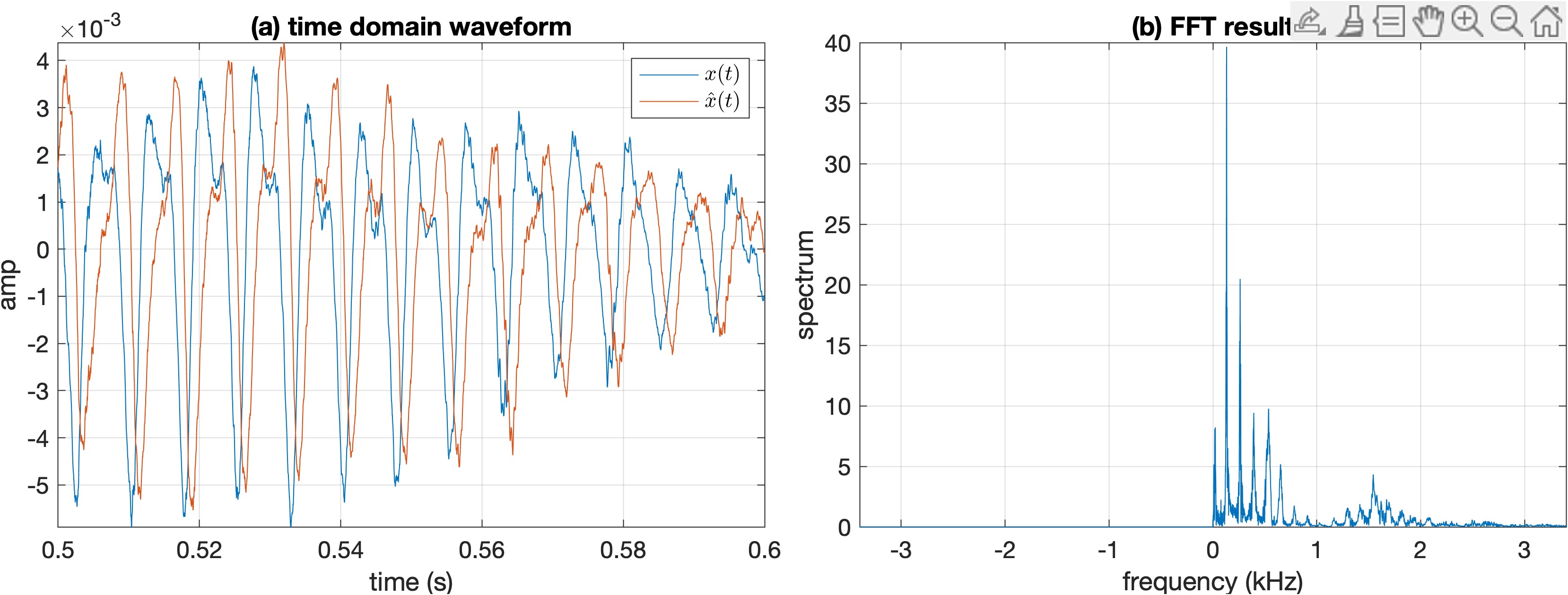（a）示例信号对应解析信号的0.5s至0.6s的时域波形，可以看到Hilbert变换的延时作用还是很明显的；（b）解析信号的FFT结果，可以看到负频率部分已经为0，正频率部分的幅度变为原来的二倍。
把这个基带信号调制到高频载波上得到
\[\begin{equation} s_a(t)=x_a(t)*e^{j2\pi f_c t} \end{equation}\]但是上面的解析带通信号是一个复信号，而现实世界中只能发送实信号。因此我们可以取这个信号的实部。根据Fourier变换的性质，对信号取实部对应的频域变化如下
\[\begin{equation} \Re\{x(t)\} \xrightarrow{\mathscr{F}} .5[X(f) + X*(-f)] \end{equation}\]可以看到这样就可以保证了频域的共轭对称性，而且正频率部分幅度减半，除此之外没有任何影响。所以我们有
\[\begin{equation} s(t)=x(t)\cos(2\pi f_c t) - \hat{x}(t)\sin(2\pi f_c t) \label{eq:hilbert_ssb} \end{equation}\]调制后的解析信号和其实部的FFT结果如下图所示
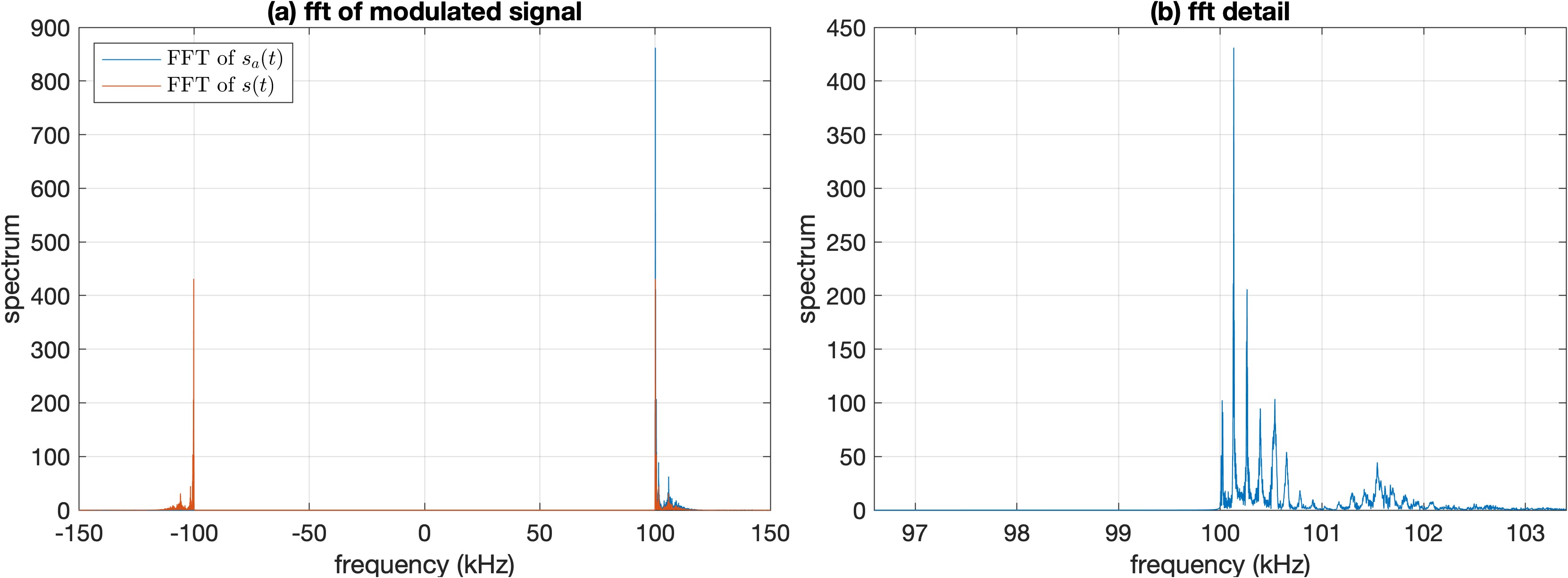（a）蓝色的线条是解析信号直接调制的结果，可以看到只有正频率部分，橙色线条为调制解析信号的实部的fft结果，可以看到其关于原点对称（实际上是共轭对称，但这里只绘制了幅度谱）（b）调制信号实部在载波频率处的结果，可以看到它只占用了上边带的频谱。
公式$\eqref{eq:hilbert_ssb}$即为将Hilbert变换应用于SSB调制中。当然除了使用Hilbert变换外，还可以通过直接滤波等其他方式进行SSB调制，在这里不再描述。
Hilbert变换与等效基带信号的关系
那么Hilbert变换与之前提到的等效基带信号有什么关系呢？首先介绍Bedrosian定理
Bedrosian 定理 如果一个低通信号和一个高通信号的频谱没有重叠，那么这两个信号的乘积的Hilbert变换是低通信号和高通信号Hilbert变换的乘积。公式描述为：$\mathcal{H}[f_{\rm LP}(t)\cdot f_{\rm HP}(t)] = f_{\rm LP}(t)\cdot \mathcal{H}[f_{\rm HP}(t)]$
回到公式$\eqref{complex_envelope}$，如果$s_I(t)$和$s_Q(t)$的足够小，那么带通信号的Hilbert变换为
\[\begin{equation} \hat{s}(t)=s_I(t)\sin(2\pi f_ct) + s_Q(t)\cos(2\pi f_c t) \end{equation}\]因而该带通信号的解析信号为
\[\begin{equation} \label{analytic_bandpass} s(t)+j\hat{s}(t)=(s_I(t)+js_Q(t))e^{j2\pi f_ct} \end{equation}\]而上式右侧正是带通信号的等效基带表示。也就是说如果一个带通信号满足Bedrosian定理中的条件（显然常见的窄带信号满足这个条件），那么它的解析信号就是其等效基带表示。因此对于一个载波频率已知的窄带信号，我们可以通过求其解析信号来得到它的等效基带信号（复包络）。
- $s(t)$的解析信号频谱只有正频率部分，这一点除了从解析信号的性质可以得到，还可以从其等效基带信号乘以$e^{j2\pi f_ct}$可以看出，这也从侧面证明了如果带通信号不满足Bedrosian定理的条件，那么也无法从带通信号的解析信号中获取其复包络。
- 等效基带信号$u(t)$是一个复信号，因此它的频谱不一定是对称的，可以考虑两种特殊情况：
- $U(f)$只有单边谱（正频率部分），此时其正交分量为同相分量的Hilbert变换，这种情况可以应用于SSB调制；
- $U(f)$共轭对称，此时$u(t)$只有实部，也就是说$s_Q(t)\equiv0$，结合公式$\eqref{complex_envelope}$，可以看到这需要$\phi(t)+\phi_0\equiv k\pi\ (k\in\mathbb{Z})$，因此只有幅度调制的时候才能满足这个条件。
Hilbert变换应用于解调器
因为Hilbert变换可以提取带通信号的复包络，而复包络中包含了被调制信号的所有信息，因此Hilbert变换可以用于解调。结合公式$\eqref{complex_envelope}$和$\eqref{analytic_bandpass}$，对于一个带通信号，其瞬时幅度和相位可以通过下式得到
\[\begin{equation} \left\{ \begin{array}{} |\alpha(t)|=\sqrt{s^2(t)+\hat{s}^2(t)}\\ \phi(t)=\arctan (\hat{s}(t)/s(t))-2\pi f_ct \end{array} \right. \end{equation}\]将之前使用的“seven”语音信号调制到100kHz的载波上，然后使用Hilbert变换解调，在SNR分别为20dB和10dB的结果如下图所示
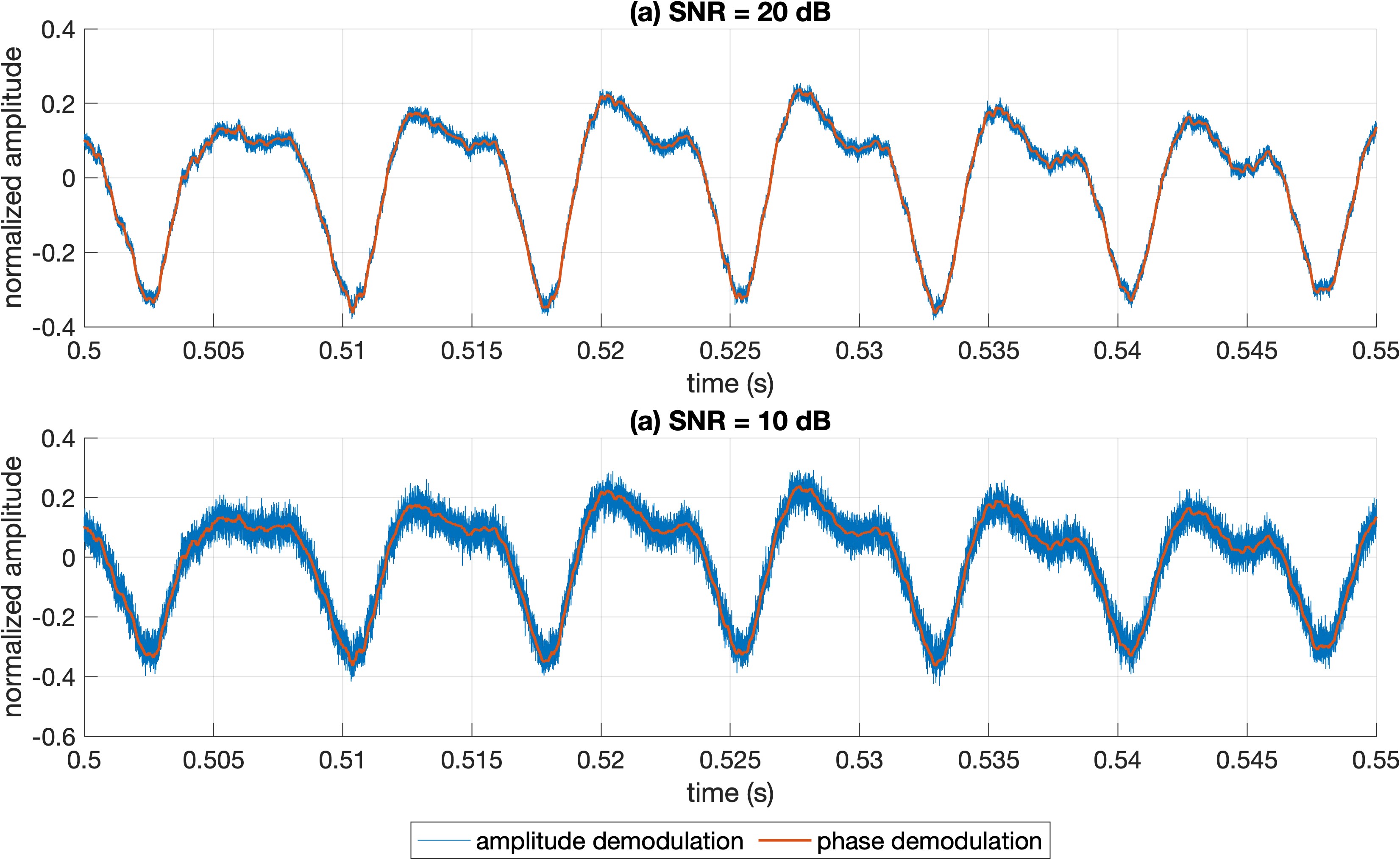（a）SNR为20dB时的解调结果；（b）SNR为10dB是的解调结果。可以看到信噪比对加载到载波幅度上的信息影响很大，而由于白噪声是非相干的，因此对于相位的解调影响不大。
应当注意的是，Hilbert变换是非因果的，因为如果把它看作一个线性系统的话，其单位冲激响应在$t<0$处也有定义。因此Hilbert变换不能实现实时解调，在实际应用中不被使用。
什么是IQ调制
我认为IQ调制是一种通用的幅度/相位调制器结构，它是公式$\eqref{complex_envelope}$的实际实现方式。下图展示了IQ调制器的基本结构。
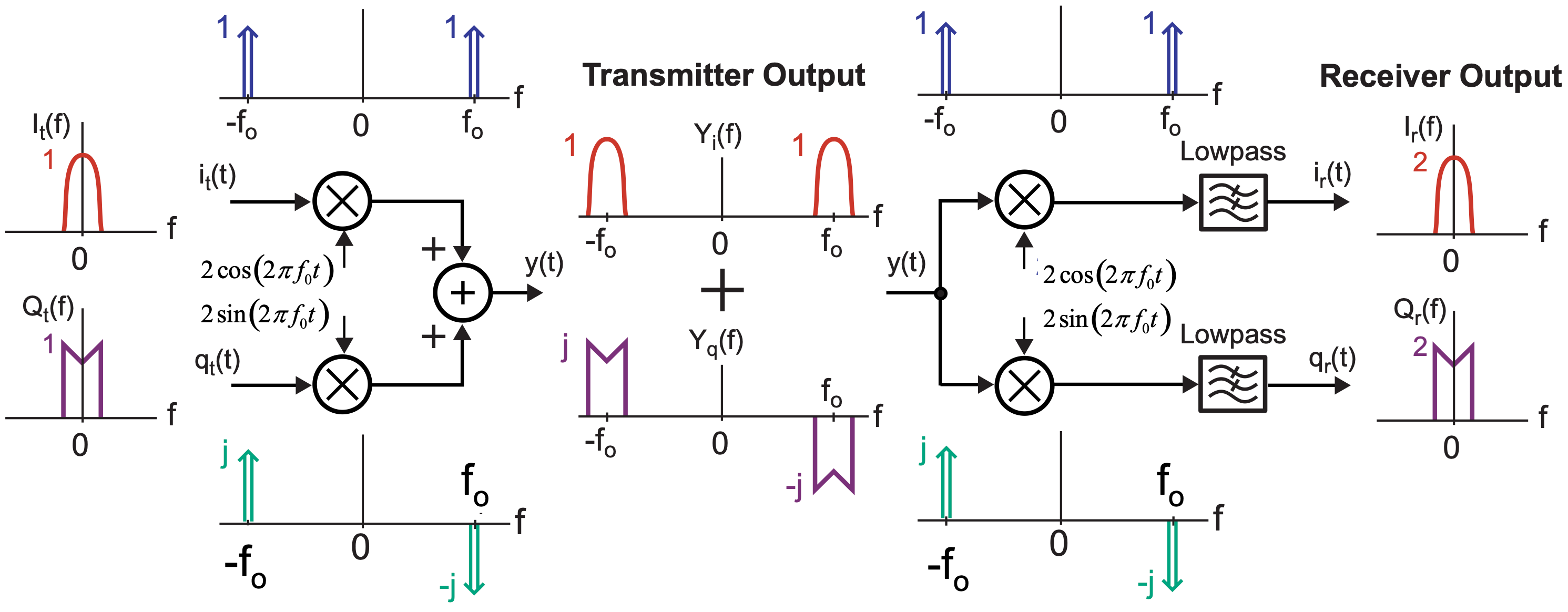IQ调制器结构以及通信过程中信号频谱变换情况。可以看到I通道和Q通道虽然在频域上是重叠的，但是由于IQ载波的正交性在解调的时候可以分辨出不同通道的信号。
做为一种调制器结构，很多种幅度/相位调制方式都可以使用IQ调制器来实现。比如说正交通道不输入信号，而只在同相通道输入模拟信号，那么这时候IQ调制器实际上是在做AM调制。如果在IQ调制器之前对数字信号进行编码和脉冲成型，那么还可以实现MPAM、MPSK和MQAM调制。作为公式$\eqref{complex_envelope}$的实际实现方式，输入IQ通道的信号以及IQ解调出来的信号可以非常方便的用复数表示。
总结
本文主要分析了复包络、Hilbert变换和IQ调制这三个涉及到复信号的概念，可以总结如以下四点：
- 引入等效基带信号的重要意义之一是降低仿真通信系统的计算和存储复杂度；
- Hilbert变换可以用来提取带通信号的等效基带信号，因此可以用来解调，但是其非因果性限制了其在实际的通信系统中的应用；
- Hilbert变换可以用于实现SSB调制；
- IQ调制是一种调制器结构，可以实现很多中具体的相位/幅度调制（如AM、MQAM）等。
参考资料
- A. Goldsmith, Wireless Communications
- Lecture 9 Analog and Digital I/Q Modulation
- The Hilbert Transform
- 为什么要用等效基带信号？
