如果给出一个函数上的一系列的离散点让你去恢复这个原函数，你会怎么做呢？实际上，这是一个函数插值问题，如果我们所选取大的差值算法不一样，那么恢复出来的函数也不一样。也就是说给定一些离散点，能够差值出无穷多个函数。
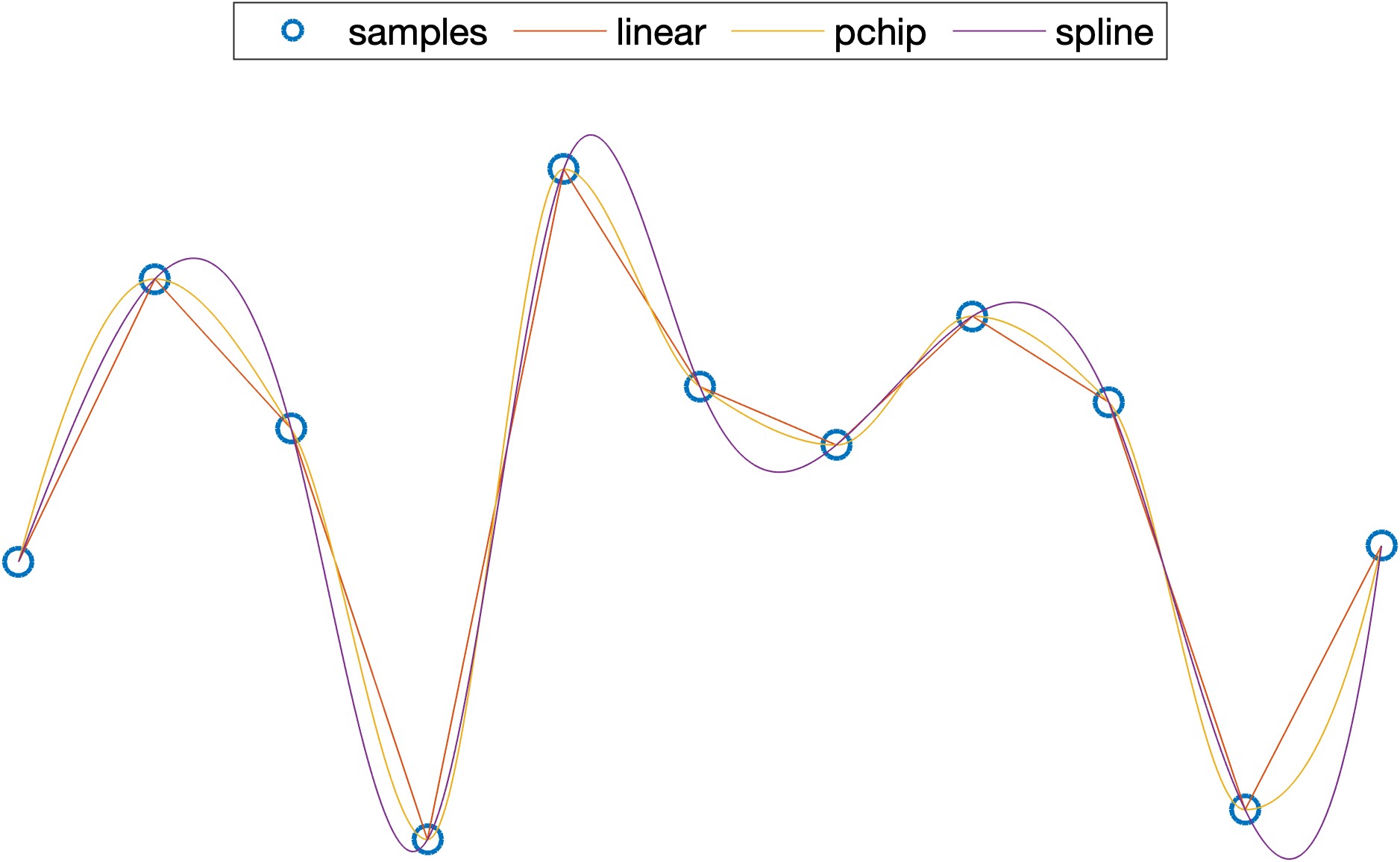
那么是不是说我们的采样就毫无意义了呢？Shannon采样定理指出，如果想从离散的均匀采样点中唯一恢复原信号，那么这个信号需要是带限信号且其带宽小于Nyquist频率（即二分之一采样频率）。这个定理想必是耳熟能详，而且其从频域理解起来非常直观，因为原始信号可以表示为
\[\begin{equation} x_p(t)=x(t)p(t) \end{equation}\]其中
\[\begin{equation} p(t)=\sum_{n=-\infty}^{+\infty}\delta(t-nT_s) \end{equation}\]为脉冲序列。因为时域乘积对应频域卷积，因此$x_p(t)$的Fourier变换为
\[\begin{equation} X_p(\omega)=\frac{1}{T_s}\sum_{k=-\infty}^{+\infty}X(\omega-k\omega_s) \end{equation}\]这个公式的几何意义就是把 $X(\omega)$ 以采样角频率 $\omega_s$ 为间隔在频率轴上无限平移。如果平移后的频谱没有重叠，那么就可以通过一个理想低通滤波器来精确复原原始信号。但上述结论在时域中就没有那么直观了——对于一个时域波形，我们只能感觉到采样间隔越小就越接近原信号，但是具体要有多小才足够是不能观察出来的。或许我们可以找一个特殊的信号来分析，然后通过这个信号来拓展到更一般的情况，这个信号就是正弦信号。
从时域理解采样定理
我们考虑对一个正弦信号进行采样
\[\begin{equation} x[n] \triangleq \cos(\omega T_s n+\phi_0)\quad n\in\mathbb{Z} \end{equation}\]其中定义 $\Omega=\omega T_s$ 为数字角频率，$\phi_0$ 为初始相位。因为正弦函数以$2\pi$为周期，因此
\[\begin{equation} \begin{aligned} \cos(\omega T_s n+\phi_0)&=\cos(\omega T_s n + 2\pi l+\phi_0)\quad\qquad l\in\mathbb{Z}\\ &=\cos(\omega T_s n+2\pi ln+\phi_0)\\ &=\cos((\omega+\frac{2\pi}{T_s}l)T_s n+\phi_0) \end{aligned} \end{equation}\]可以看到如果只用离散的采样点表示这个正弦信号的话，那么所有频率满足 $f_a=f+lf_s$ 的正弦信号都有着完全相同的离散表示，这种现象称为aliasing。另外根据三角函数的性质，我们还可以得到
\[\begin{equation} \begin{aligned} \cos(\omega T_s n+\phi_0)&=\cos(2\pi l-\omega T_sn-\phi_0)\\ &=\cos(2\pi(lf_s-f)T_sn-\phi_0) \end{aligned} \end{equation}\]通过平移 $2\phi_0$ 相位就可以得到与原频率离散点相同的信号，因此 $lf_s-f$ 也是aliasing频率。假设我们将采样频率固定为1kHz，当信号的实际频率从0渐渐增加时，它和aliasing频率在频率轴上的分布变化如下图所示
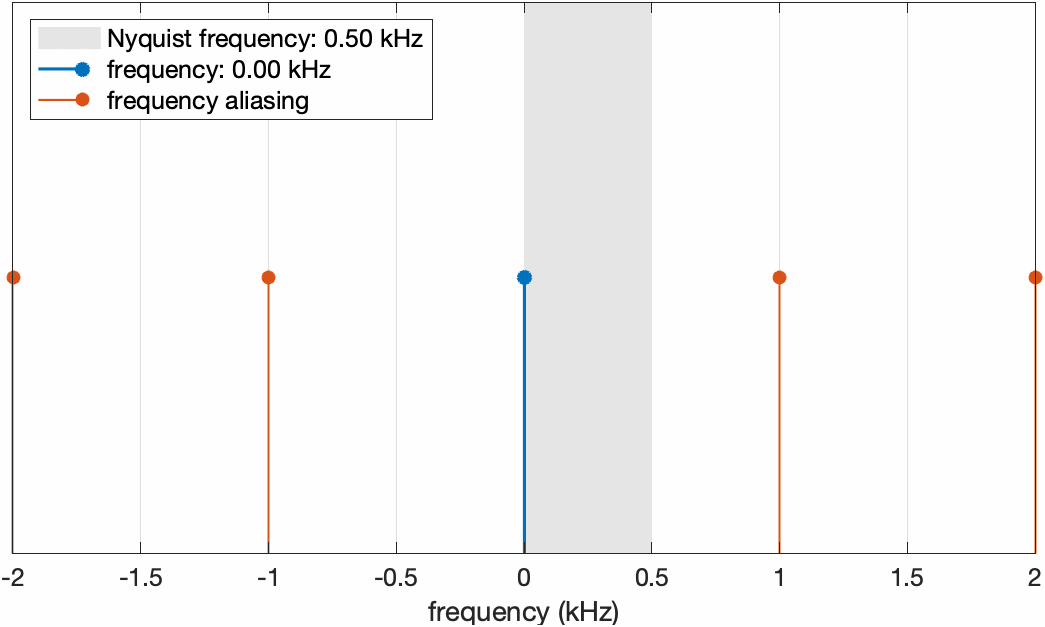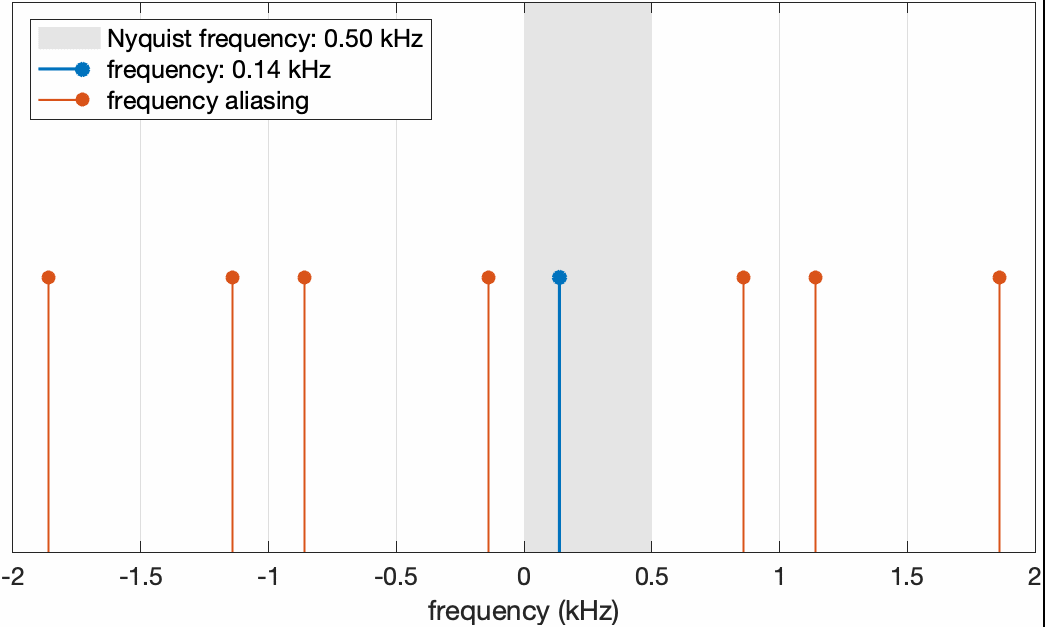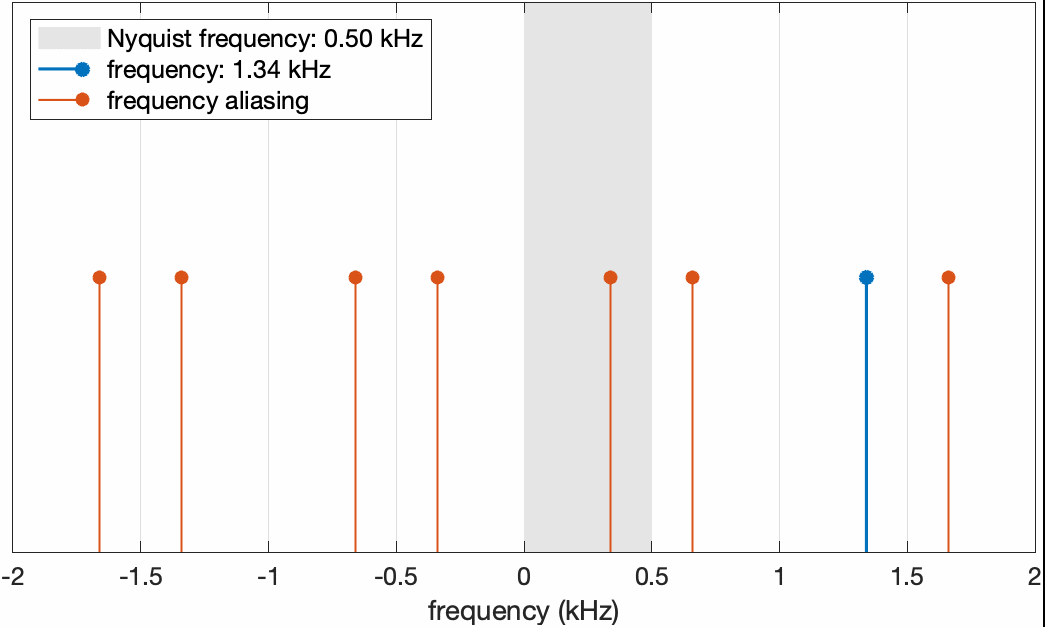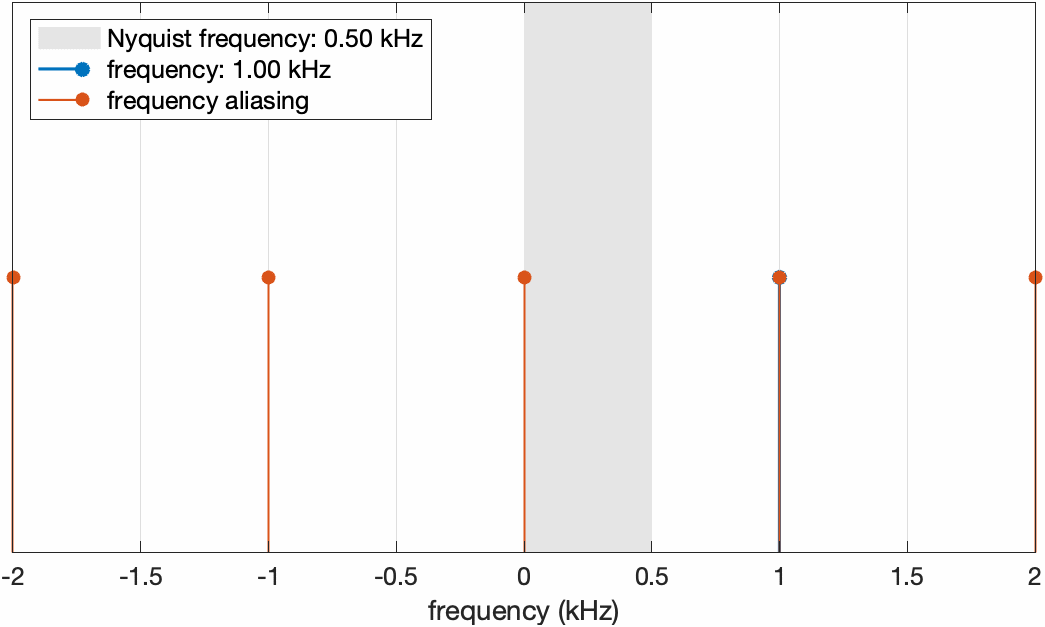固定采样频率为1kHz（对应Nyquist频率0.5kHz），将信号频率从0开始增加。可以看到当信号频率超过Nyquist频率之后，aliasing频率替代了原始频率的位置。
如果我们固定信号的频率，把采样频率从小到大的增加，那么这些aliasing频率和信号频率的变化关系如下图所示
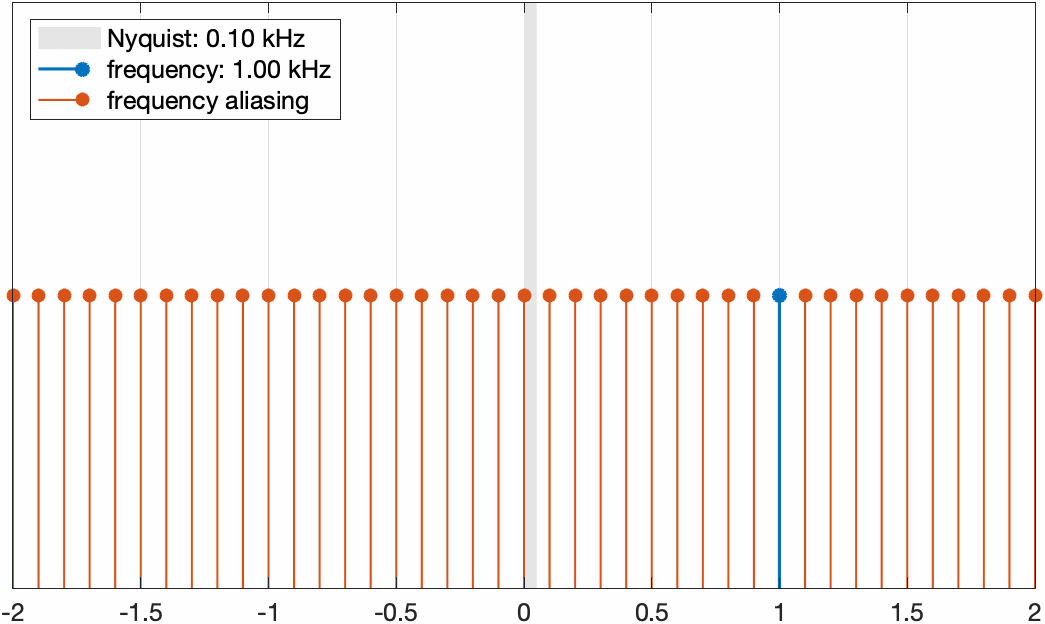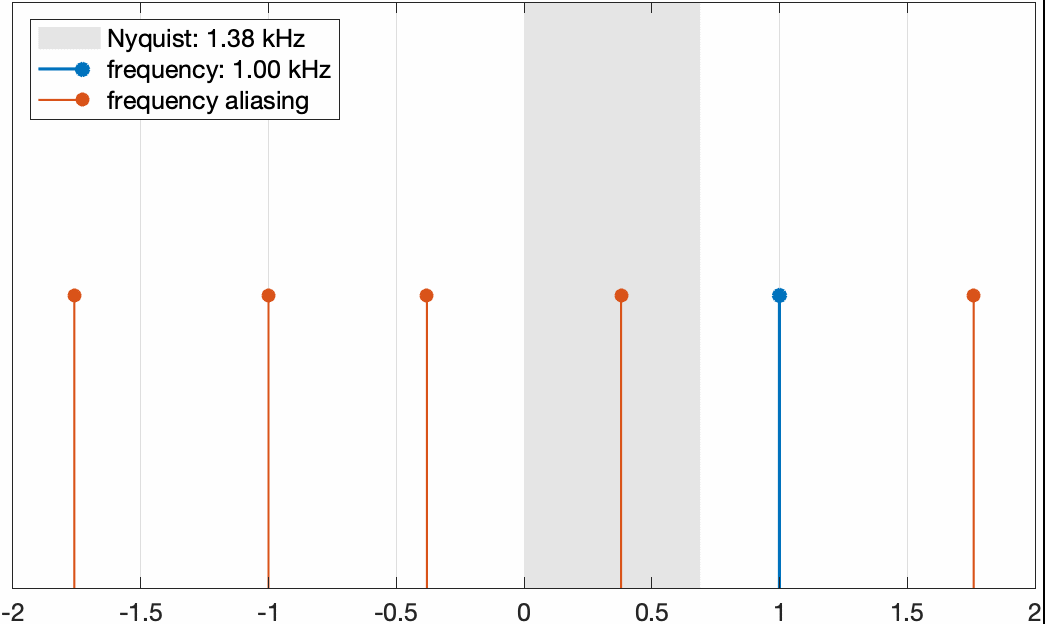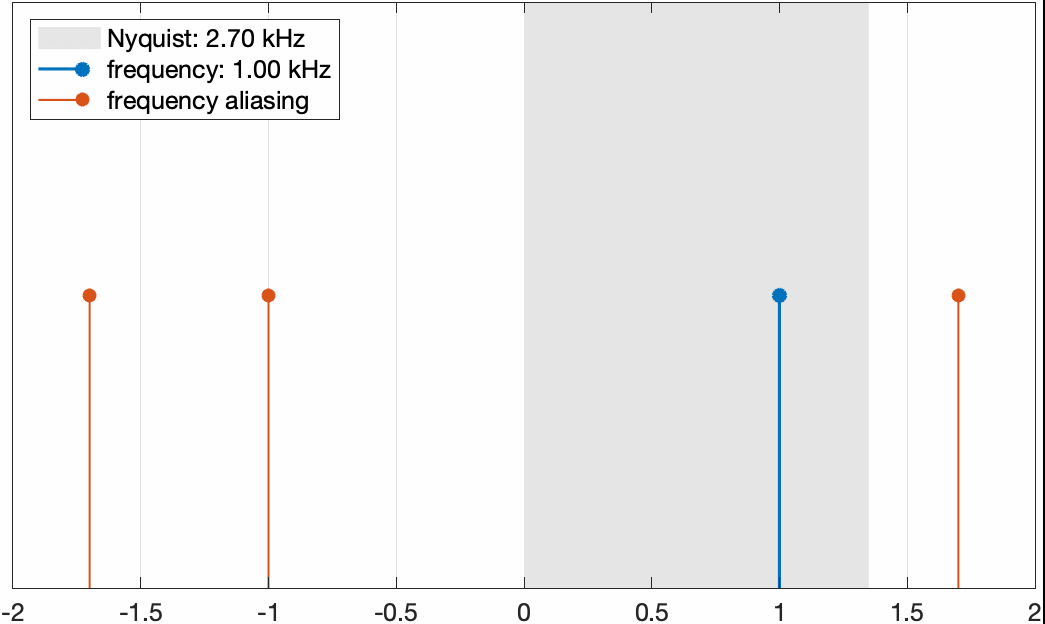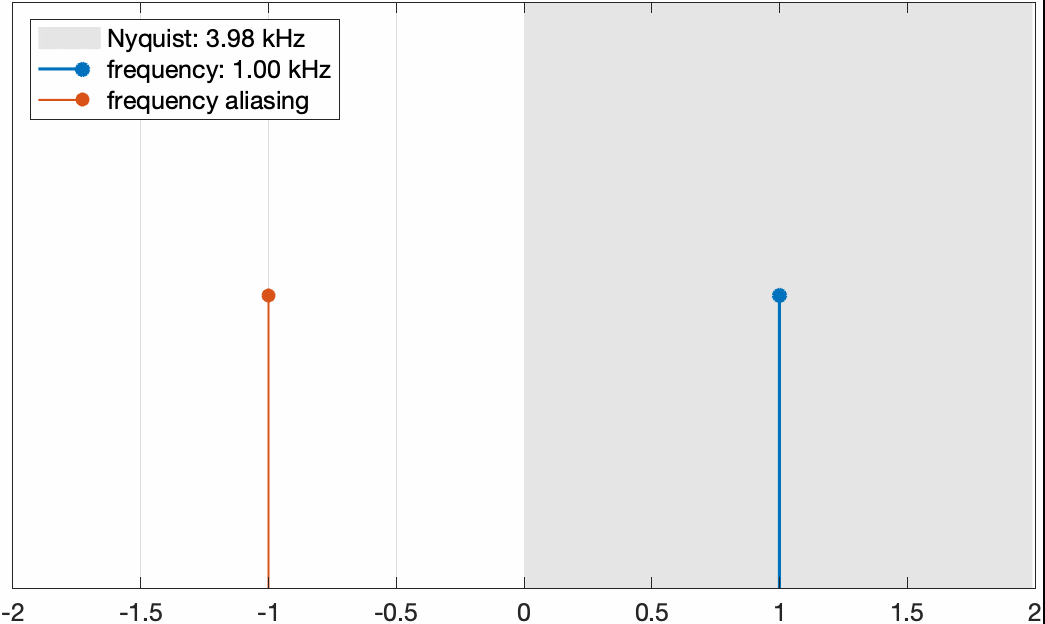固定信号频率为1kHz，把采样频率逐渐增加。可以看到当Nyquist频率小于信号频率时，在0到信号频率内存在aliasing频率，而当Nyquist频率大于信号频率时，则不存在aliasing频率。
我们知道任何一个信号都可以表示为所有频率的正弦函数的叠加。由此可见如果一个低通信号的最高频率为$f_\max$，那么它不产生aliasing频率需要满足 $f_s-f_\max>f_\max$ 也就是 $f_s>2f_\max$。
空域采样
我们知道信息的一种载体是波，比如电磁波或者声波。一个沿 $x$ 轴方向传播的平面波可以表示为
\[\begin{equation} x(t)=\exp(j(\omega t - k x)) \label{eq:wave_equ} \end{equation}\]这个方程有几个需要说明的地方：
- 在现实世界中只存在实数，因此实际的波应当是 $\Re[x(t)]$ ，为了方便起见这里默认采用波的复数表示；
- 指数部分的表示有很多不同的惯例，这里采用的是 $\omega t - k x$，此时指数部分我认为物理意义比较明确：因为现实世界中角频率和波数都是正数，所以从时间角度来看，对于一个固定的位置 $x$ ，其相位随着时间的增加而增加；从位移角度来看，对于一个固定的时间，相位随着距离的增大而减小，这说明波是沿坐标轴方向传播的；
- 沿坐标轴反方向传播的指数部分应当表示为 $\omega t + kx$，但在这里为了方便起见我们允许波数为负数，代表沿坐标轴反方向传播。
当我们在空间中放置一个传感器的时候，实际上就是对这个波进行时间轴上的采样，我们得不到关于波的位置信息。但是如果我们在空间中同时放置多个传感器，当波以不同的时间分别到达这些传感器时，我们就可以通过这些波之间的相位差信息来获得波的空间信息。
那么多个传感器应该如何放置呢？我们可以很直觉的想象到肯定是放得越近、越多越好，考虑极端情况整个空间都布满传感器时，我们就能得到其全部信息。当这些传感器之间的距离逐渐被拉开，应当也会存在一个类似于Nyquist频率的界限。为了推导出这一界限，现在我们考虑平面波照射到ULA（Uniform Line Array）的情况。
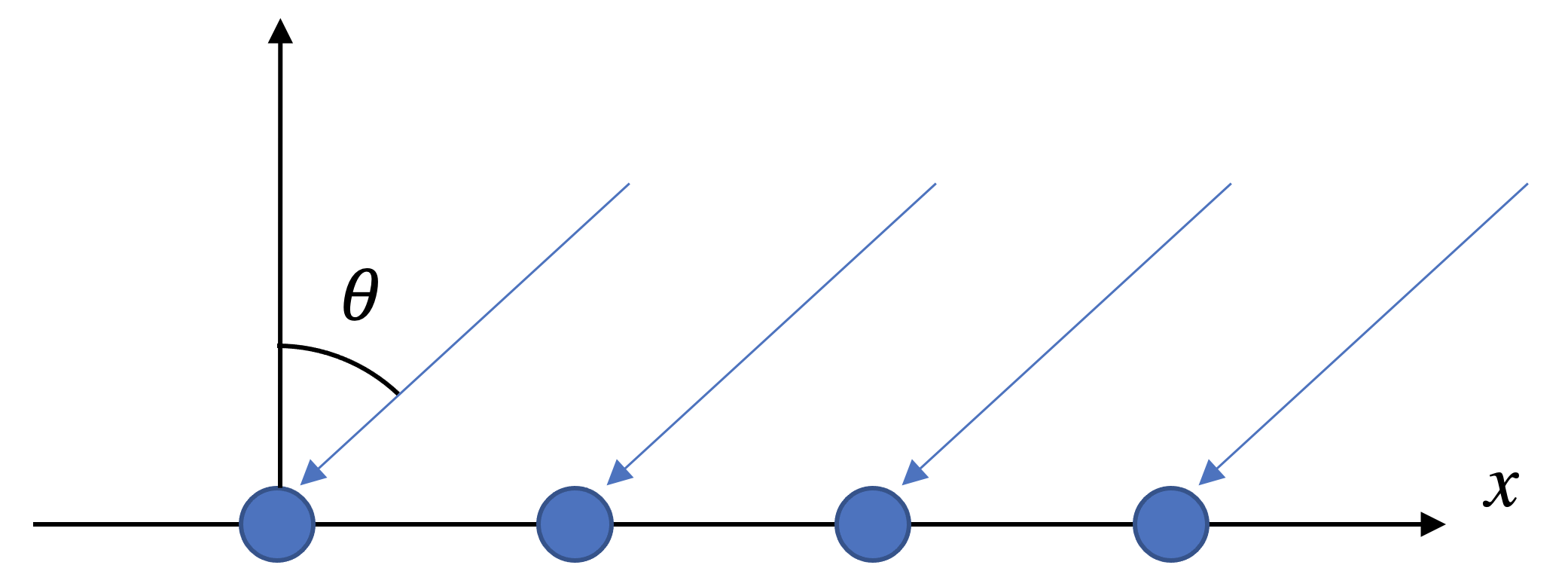远场平面波照射到ULA示意图。波的入射角为 $\theta$，按照惯例，从左手边到右手边角度从 $-90^\circ$ 增加到 $90^\circ$。
当我们使用ULA来采样一个平面波的时候，可以将波动公式$\eqref{eq:wave_equ}$中的时间考虑为一个常数，那么它在空间中就是一个正弦分布。对于ULA，我们这里只考虑二维的情况（ULA在第三个维度上存在模糊）。在传感器所在的轴上，我们能够采样到的波的波数实际上是波数在该轴上的投影，因此不同的入射角度对应的波数不同，其关系为
\[\begin{equation} k_x = -k\sin\theta \end{equation}\]当入射角为 $0^\circ$ 时，投影到 $x$ 轴上的波数为0，可以看作直流。而随着入射角度增大，当最大到达 $\pm90^\circ$ 时波数达到最大。假设我们的阵元间距为 $x_s$ ，那么在零时刻我们采样到的波可以表示为 $\cos(-k_xx_sn)$，同样我们有
\[\begin{equation} \begin{aligned} \cos(-k_xx_sn)&=\cos(-k_xx_sn+2\pi l)\qquad\quad l\in\mathbb{Z}\\ &=\cos(-k_xx_sn+2\pi ln)\\ &=\cos(-(k_x-l\frac{2\pi}{x_s})x_sn) \end{aligned} \end{equation}\]我们可以定义采样波数为 $k_s=2\pi/x_s$，那么类似于时域的分析同样我们有aliasing波数 $k_a=k+lk_s$ 以及 $k_a=lk_s-k$。如果传感器放置得不够密集，那么就会存在aliasing波数，也就是说会有若干个波数有同样的采样结果，而这样带来最终后果就是我们无法区分这些波数所对应的入射角，并且该临界距离为 $\lambda/2$。
假设有平面波的波长为 $1~\text{m}$，如果我们取传感器间距为 $1.5~\text{m}$ 并放置4个传感器来进行空间采样，当它从ULA的最左侧转移到最右侧时，投影到ULA的平面波以及传感器的采样结果如下图所示
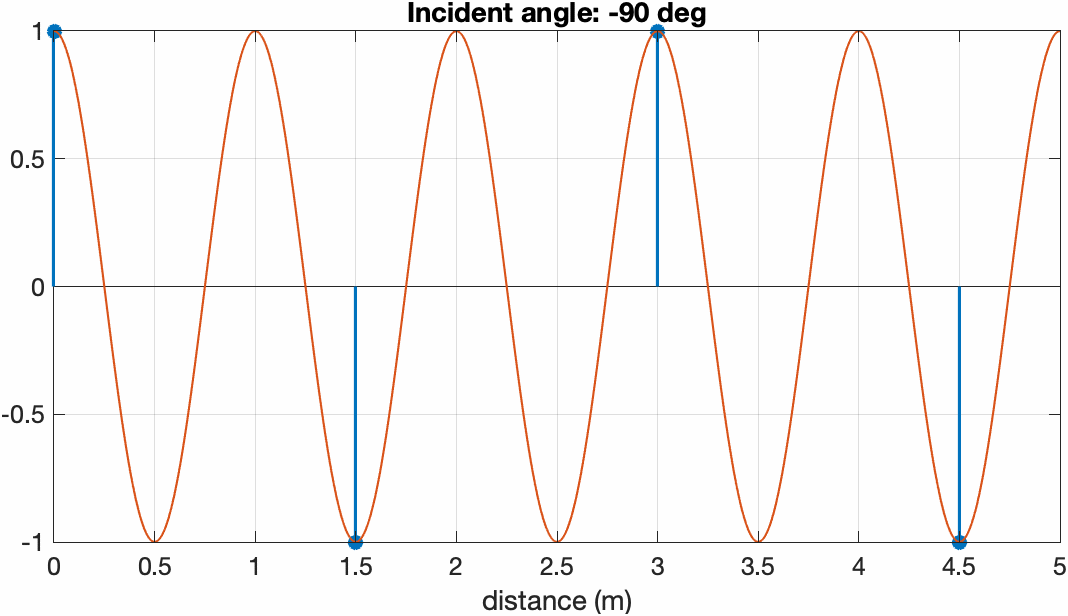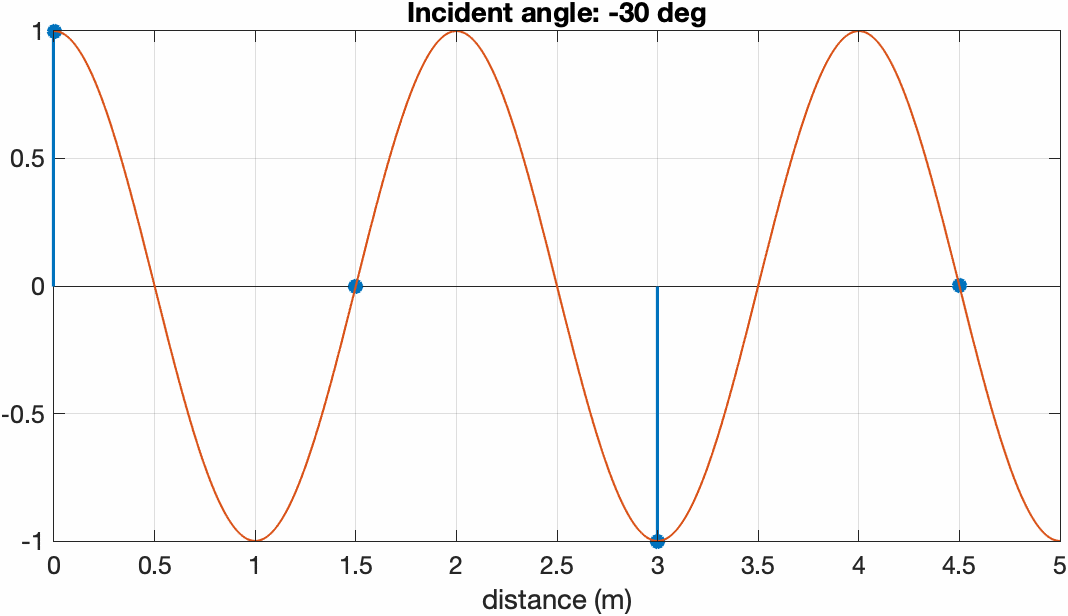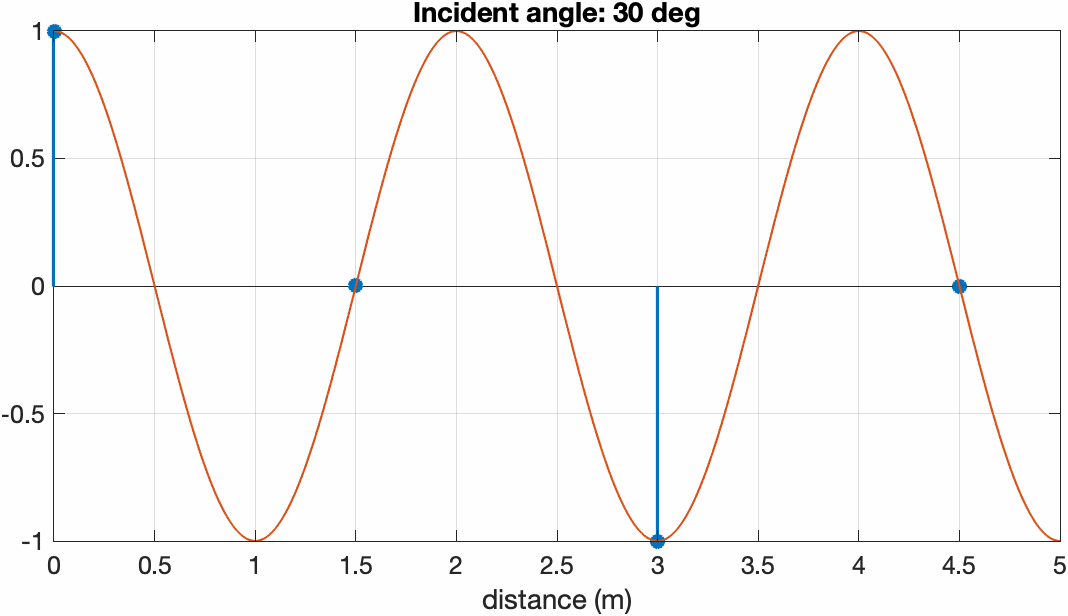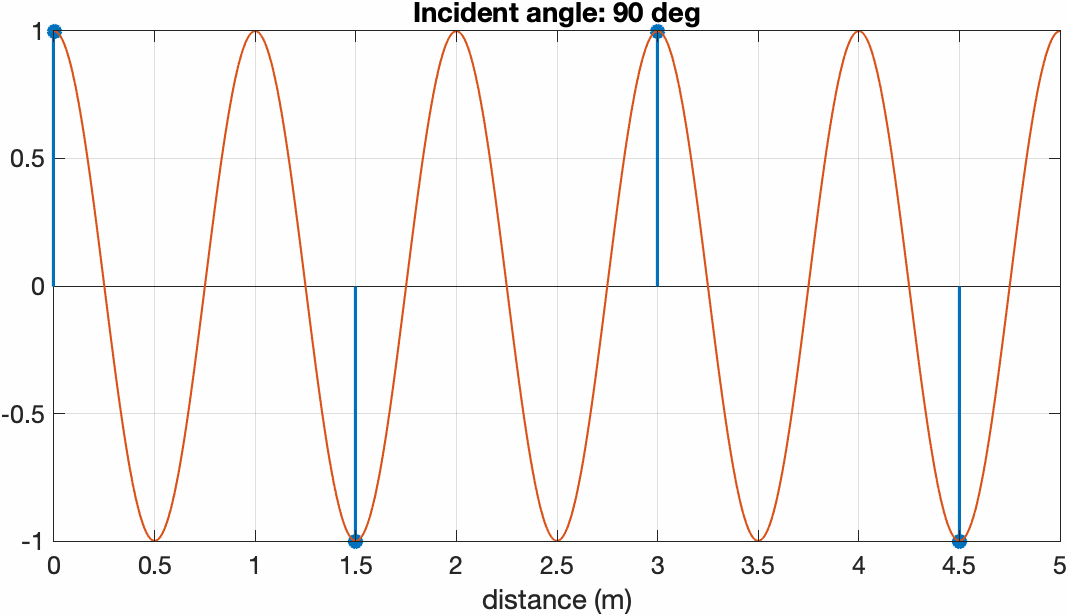入射角从 $-90^\circ$ 增加到 $+90^\circ$ 时ULA采样到波前。可以看到当平面波在端射方向时波的波长最短，对应高频；越靠近边射方向波长越长，当角度为 $0^\circ$ 时可以理解为直流。
此时不满足阵元间距小于半波长的条件，会出现aliasing波数，会有多个入射角度产生相同的采样结果。
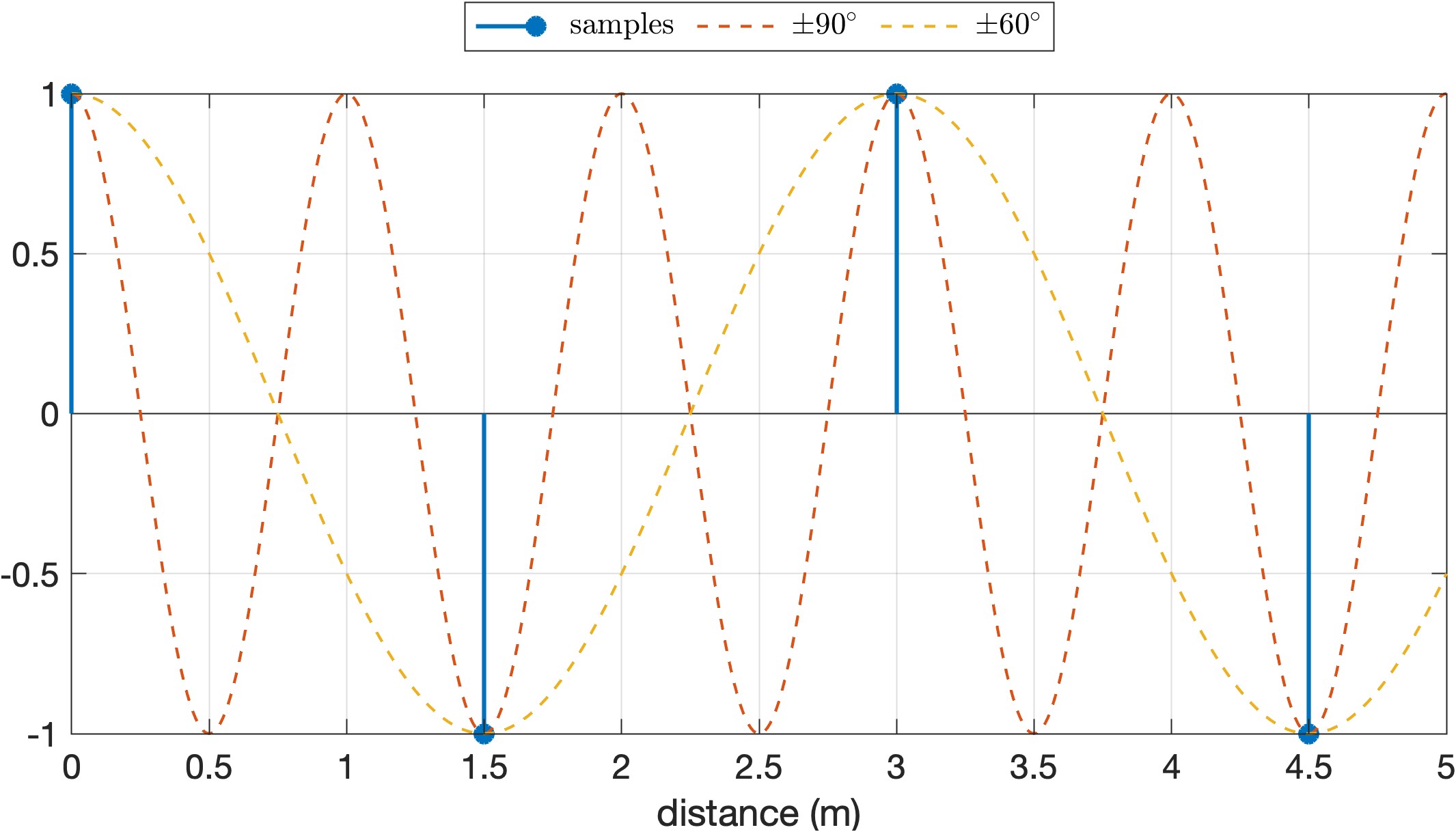波长为 $1~\text{m}$ 阵元间距为 $1.5~\text{m}$ 时有多个角度会产生相同的空间采样结果。
总结
本文主要说明了香农采样定理的时域理解方法，并将这个方法延拓到空间采样定理上。空间采样与时间采样类似存在一个能够完全恢复空域信号的临界点，这个临界点就是最高频率的半波长。
参考资料
- H. L. V. Trees, Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory, 1st edition.
